Infering Partially Observable Markov Processes with Iterative Particle Filtering

Excellent talk by Ed Ionides at UC Davis today (led me to miss Weds session of Data to Knowledge).

Ed Ionides

six problems of Bjonstead and Grenfell: an appeal for arbitrary nonlinear partially observed vector valued stochastic models.
POMP doesn’t mix well in the winbugs.

simulation-based algorithm (plug-and-play)

Think of a process being defined by:

  • rprocess()
  • dprocess()
  • rmeasure()
  • dmeasure()

In general we need some subset of these processes:

type rprocess dprocess rmeasure dmeasure
iterative filtering X X
Lui-West SCM X X
EM by SCM X X X
MCMC X X
Nonlin forecasting X X
Particle MCMC X X
Probe matching X X

Bayesian plug-and-play

Non-Bayesian

“Likelihood-free” inference – i.e. don’t have the likelihood equation unlike MCMC, EM need dprocess()

  • Compare to optimization “gradient-free” methods.
  • or to Keverkidis “equation-free” (Kevrekidis et. al. 2003) Approximate Bayesian methods and simulated moment methods lead to loss of statistical efficiency Iterated filtering enables almost exact likelihood-based inference.

ODEs have been plug-and-play (numerical) for a long time. We want this to be true for SDEs as well.

Filtering

  • Think “Kalman filter”. Particle filter is a simulated approximation approach for the likelihood function.
  • Iterative filtering is a much more clever way to search for the best fit model than some traditional optimization routine that wants a smooth likelihood function.

Theorem: derivative of the log-likelihood is the small-noise limit of a weighted average of local filtering. In:

Scientists like life on the edge of identifiability, > Minimal complexity acceptable to scientsits approx maximimal complexity acceptable to available data

References

  • Christophe Andrieu, Arnaud Doucet, Roman Holenstein, (2010) Particle Markov Chain Monte Carlo Methods. Journal of The Royal Statistical Society: Series B (Statistical Methodology) 72 10.1111/j.1467-9868.2009.00736.x
  • E. L. Ionides, C. Breto, A. A. King, (2006) Inference For Nonlinear Dynamical Systems. Proceedings of The National Academy of Sciences 103 10.1073/pnas.0603181103
  • Edward L. Ionides, Anindya Bhadra, Yves Atchadé, Aaron King, (2011) Iterated Filtering. The Annals of Statistics 39 10.1214/11-AOS886
  • Bruce E. Kendall, Cheryl J. Briggs, William W. Murdoch, Peter Turchin, Stephen P. Ellner, Edward McCauley, Roger M. Nisbet, Simon N. Wood, (1999) Why do Populations Cycle? A Synthesis of Statistical And Mechanistic Modeling Approaches. Ecology 80 10.1890/0012-9658(1999)080[1789:WDPCAS]2.0.CO;2

  • Simon N. Wood, (2010) Statistical Inference For Noisy Nonlinear Ecological Dynamic Systems. Nature 466 10.1038/nature09319

  • E. L. Ionides, C. Breto, A. A. King, (2006) Inference For Nonlinear Dynamical Systems. Proceedings of The National Academy of Sciences 103 10.1073/pnas.0603181103
  • T. Toni, D. Welch, N. Strelkowa, A. Ipsen, M. P.H Stumpf, (2009) Approximate Bayesian Computation Scheme For Parameter Inference And Model Selection in Dynamical Systems. Journal of The Royal Society Interface 6 10.1098/rsif.2008.0172

  • Ioannis Kevrekidis, William Gear, James Hyman, Panagiotis Kevrekidid, Olof Runborg, Constantinos Theodoropoulos, (2003) Equation-Free, Coarse-Grained Multiscale Computation: Enabling Mocroscopic Simulators to Perform System-Level Analysis. Communications in Mathematical Sciences https://projecteuclid.org/euclid.cms/1119655353

Exploring Iterative Filtering in POMP

my example exploration, following the introductory vignette.

Note that the iterative filtering algorithm took a little over 16 minutes on ten processors on the farm cluster. pomp does not provide any parallelization. Particles must communicate at each iteration. With tight communication loops, could probably get substantial acceleration on MPI or GPU.

(Would be interesting to drive the simulation with Gillespie algorithm, something richer than a crude discritization. Depending on timescale, may result in very computationally intensive requirements).

require(pomp)
gompertz.proc.sim <- function(x, t, params, delta.t, ...) {
    r <- params["r"]
    K <- params["K"]
    sigma <- params["sigma"]
    X <- x["X"]  # the state at time t:
    ## generate a log-normal random variable:
    eps <- exp(rnorm(n = 1, mean = 0, sd = sigma))
    ## compute the state at time t+delta.t:
    S <- exp(-r * delta.t)
    c(X = unname(K^(1 - S) * X^S * eps))
}
gompertz.meas.sim <- function(x, t, params, ...) {
    tau <- params["tau"]
    X <- x["X"]  # state at time t:
    y <- c(Y = unname(rlnorm(n = 1, meanlog = log(X), sd = tau)))
}

create a container of class pomp to hold the model and data.

gompertz <- pomp(data = data.frame(time = 1:100, Y = NA), times = "time", 
    rprocess = discrete.time.sim(step.fun = gompertz.proc.sim, delta.t = 1), 
    rmeasure = gompertz.meas.sim, t0 = 0)

Parameters and inital condition:

theta <- c(r = 0.1, K = 1, sigma = 0.1, tau = 0.1, X.0 = 1)
gompertz <- simulate(gompertz, params = theta)
plot(gompertz, variables = "Y")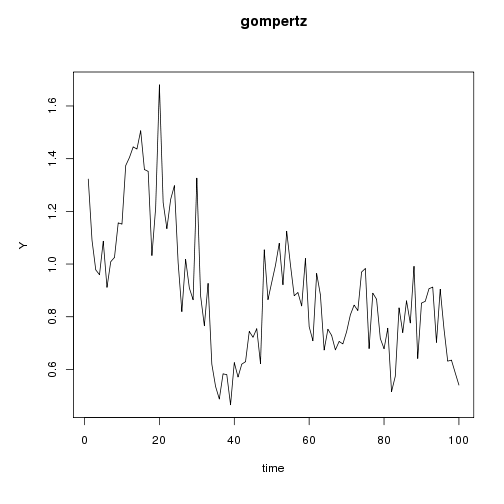
plot of chunk simulate
plot of chunk simulate

Likelihood using a particle filter (sequential Monte Carlo) requires the measurement density (but not the process density).

gompertz.meas.dens <- function(y, x, t, params, log, ...) {
    tau <- params["tau"]
    ## state at time t:
    X <- x["X"]
    ## observation at time t:
    Y <- y["Y"]
    ## compute the likelihood of Y|X,tau
    dlnorm(x = Y, meanlog = log(X), sdlog = tau, log = log)
}

Stick the new function into our container:

gompertz <- pomp(gompertz, dmeasure = gompertz.meas.dens)

Then we get a point estimate of the likelihood,

pf <- pfilter(gompertz, params = theta, Np = 1000)
logLik(pf)
[1] 49.29

Iterated filtering

We will do this in the transformed variable space, so we add our transformation method to the container:

gompertz <- pomp(gompertz, parameter.transform = function(params, 
    ...) {
    exp(params)
}, parameter.inv.transform = function(params, ...) {
    log(params)
})

Now we’re ready for an iterated-filtering run. This is gonna be slow, so let’s set up a parallel architecture first:

require(snowfall)
sfInit(parallel = TRUE, cpu = 10)
rep <- function(dummy_index) {
    estpars <- c("r", "sigma", "tau")
    theta.guess <- coef(gompertz)
    theta.guess[estpars] <- rlnorm(n = length(estpars), meanlog = log(theta.guess[estpars]), 
        sdlog = 1)
    mif(gompertz, Nmif = 100, start = theta.guess, transform = TRUE, pars = estpars, 
        rw.sd = c(r = 0.02, sigma = 0.02, tau = 0.05), Np = 2000, var.factor = 4, 
        ic.lag = 10, cooling.factor = 0.999, max.fail = 10)
}
sfExportAll()
system.time(mf <- sfSapply(1:10, rep))
   user  system elapsed 
   0.02    0.00 1037.39

Average parameter estimates (compare to theta)

theta.mif <- apply(sapply(mf, coef), 1, mean)
theta.mif
      r       K   sigma     tau     X.0 
0.04385 1.00000 0.09647 0.10495 1.00000

Evaluating the log-likelihoods at the convergent parameters requires the particle filter. This line applies the particle filter to each of the parameter estimates

loglik.mif <- replicate(n = 10, logLik(pfilter(mf[[1]], params = theta.mif, 
    Np = 10000)))
bl <- mean(loglik.mif)
loglik.mif.est <- bl + log(mean(exp(loglik.mif - bl)))
loglik.mif.se <- sd(exp(loglik.mif - bl))/exp(loglik.mif.est - bl)
c(est = loglik.mif.est, se = loglik.mif.se)
     est       se 
51.45397  0.09316

“True” uses the original model and coefficients rather than the estimated one, but still approximates the log.likelihood using particle filtering

loglik.true <- replicate(n = 10, logLik(pfilter(gompertz, params = coef(gompertz), 
    Np = 10000)))
loglik.true.est <- bl + log(mean(exp(loglik.true - bl)))
loglik.true.se <- sd(exp(loglik.true - bl))/exp(loglik.true.est - 
    bl)
c(est = loglik.true.est, se = loglik.true.se)
    est      se 
50.0128  0.1062