Null Distribution Width Minor Puzzle

A quick foray into trying to understand why I see the wider distribution (though still symmetric) in the null of the OU model then in the null from the Allee model in the Prosecutor’s fallacy.

Load the original run of the ou model and increase the nulldt data frame to use all points instead of a sample of length 5000

load("beer_run.rda")

ou_dat <- dat
ou_null <- nulldat
#ou_null_ts <- nulldt

null <- timeseries #[1000:6010,]
null <- as.data.frame(cbind(time = 1:dim(null)[1], null))
ndf <- melt(null, id="time")
names(ndf) = c("time", "reps", "value")
levels(ndf$reps) <- 1:length(levels(ndf$reps)) # use numbers for reps instead of V1, V2, etc
nulldt <- data.table(ndf)
ou_null_ts <- nulldt

Plot the final distribution of indicator statistics, showing the width of the null,

ggplot(dat) + geom_histogram(aes(value, y=..density..), binwidth=0.3, alpha=.5) +
 facet_wrap(~variable) + xlim(c(-1, 1)) + 
  geom_density(data=nulldat, aes(value), adjust=2) + xlab("Kendall's tau") + theme_bw()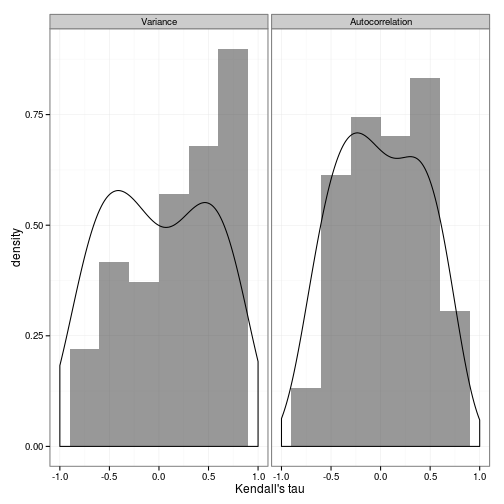
plot of chunk unnamed-chunk-4
plot of chunk unnamed-chunk-4

Load the allee model and rename variables appropriately,

load("comment_run.rda")
allee_dat <- dat
allee_null <- nulldat
allee_null_ts <- nulldt

For the Allee model, also plot the final distribution of indicator statistics, showing the width of the null,

ggplot(dat) + geom_histogram(aes(value, y=..density..), binwidth=0.3, alpha=.5) +
 facet_wrap(~variable) + xlim(c(-1, 1)) + 
  geom_density(data=nulldat, aes(value), adjust=2) + xlab("Kendall's tau") + theme_bw()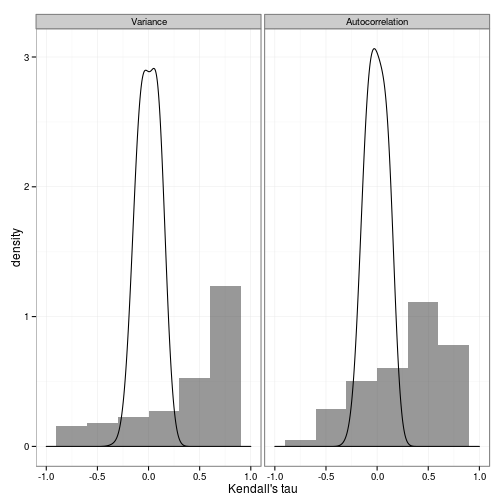
plot of chunk unnamed-chunk-6
plot of chunk unnamed-chunk-6

Tidy the data and plot a single replicate from each. Note the OU process has the correspondingly much wider null distribution due to

allee_x <- subset(allee_null_ts, reps==1)
ou_x <- subset(ou_null_ts, reps==1)
allee_x <- data.frame(time = allee_x$time, value = allee_x$value)
ou_x <- data.frame(time = ou_x$time, value = ou_x$value)

ggplot(allee_x, aes(time, value)) + geom_point()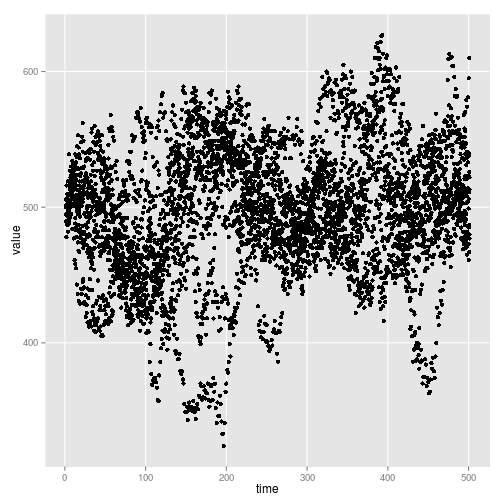
plot of chunk unnamed-chunk-7
plot of chunk unnamed-chunk-7
ggplot(ou_x, aes(time, value)) + geom_point()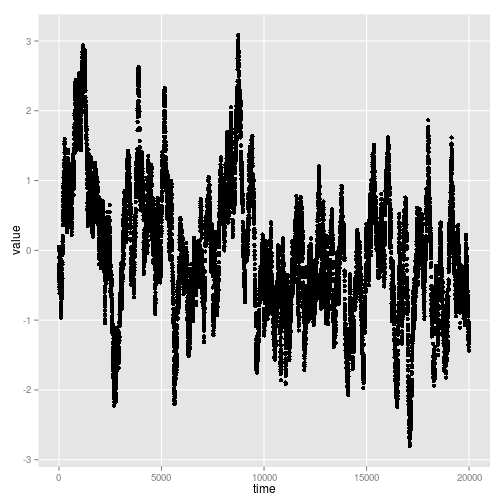
plot of chunk unnamed-chunk-7
plot of chunk unnamed-chunk-7

Note that subsampling the data at coarser interval doesn’t matter

warningtrend(ou_x[seq(1, length(ou_x$value),by=50),], window_var)
    tau 
-0.5527

Nor does scaling matter (recall Kendall’s \(tau\) is a rank-correlation test)

warningtrend(data.frame(time=ou_x$time, value=(ou_x$value+1)*500), window_var)
    tau 
-0.5516 
warningtrend(data.frame(time=ou_x$time, value=ou_x$value), window_var)
    tau 
-0.5516

Lengthening the sample suggests the sampling is not long enough to have converged in distribution of this statistic. Computing on this fine sampling resolution over adequate length of time quickly becomes prohibitive.

sapply(seq(1000, 20000, by=1000), function(i) warningtrend(ou_x[1:i,], window_var))
       tau        tau        tau        tau        tau        tau 
 0.1802475 -0.0832527  0.6365570  0.1787726 -0.1747774 -0.5295226 
       tau        tau        tau        tau        tau        tau 
-0.5403782 -0.6790710 -0.6114706 -0.2950858 -0.0444861  0.0006919 
       tau        tau        tau        tau        tau        tau 
-0.2579410 -0.5220490 -0.6439519 -0.6221482 -0.5545048 -0.5134236 
       tau        tau 
-0.5265975 -0.5515807