See also:
- https://www.carlboettiger.info/2012/12/20/results-comparing-gp-to-parametric.html
Example with fixed priors on hyperparameters, fixed model type.
#inv gamma has mean b / (a - 1) (assuming a>1) and variance b ^ 2 / ((a - 2) * (a - 1) ^ 2) (assuming a>2)
s2.p <- c(5,5)
tau2.p <- c(5,1)
d.p = c(10, 1/0.1, 10, 1/0.1)
nug.p = c(10, 1/0.1, 10, 1/0.1) # gamma mean
s2_prior <- function(x) dinvgamma(x, s2.p[1], s2.p[2])
tau2_prior <- function(x) dinvgamma(x, tau2.p[1], tau2.p[2])
d_prior <- function(x) dgamma(x, d.p[1], scale = d.p[2]) + dgamma(x, d.p[3], scale = d.p[4])
nug_prior <- function(x) dgamma(x, nug.p[1], scale = nug.p[2]) + dgamma(x, nug.p[3], scale = nug.p[4])
beta0_prior <- function(x, tau) dnorm(x, 0, tau)
beta = c(0)
priors <- list(s2 = s2_prior, tau2 = tau2_prior, beta0 = dnorm, nug = nug_prior, d = d_prior, ldetK = function(x) 0)profit = function(x,h) pmin(x, h)
delta <- 0.01
OptTime = 20 # stationarity with unstable models is tricky thing
reward = 0
xT <- 0f <- RickerAllee
# c(5, 10, 5) is 2-cycle, c(5.5, 10, 5) is 6 cycle, 5.3 is about 4
p <- c(2, 10, 5)
K <- 10
allee <- 5sigma_g <- 0.05
sigma_m <- 0.0
z_g = function() rlnorm(1, 0, sigma_g)
z_m = function() 1+(2*runif(1, 0, 1)-1) * sigma_m
x_grid <- seq(0, 1.5 * K, length=101)
h_grid <- x_gridWith parameters 2, 10, 5.
seed_i <- 1
Xo <- K # observations start from
x0 <- Xo # simulation under policy starts from obs <- sim_obs(Xo, z_g, f, p, Tobs=35, nz=15,
harvest = sort(rep(seq(0, .5, length=7), 5)), seed = seed_i) alt <- par_est(obs, init = c(r=p[1], K=mean(obs$x), s=sigma_g))
est <- par_est_allee(obs, f, p, init = c(2, mean(obs$x), 2, s = sigma_g))Which estimates a Ricker model with \(r =\) 2, \(K =\) 6.77, and the Allen allee model with \(r =\) 2, \(K =\) 6.77 and \(C =\) 2.
gp <- bgp(X=obs$x, XX=x_grid, Z=obs$y, verb=0,
meanfn="constant", bprior="b0", BTE=c(2000,16000,2),
m0r1=FALSE, corr="exp", trace=TRUE,
beta = beta, s2.p = s2.p, d.p = d.p, nug.p = nug.p, tau2.p = tau2.p,
s2.lam = "fixed", d.lam = "fixed", nug.lam = "fixed", tau2.lam = "fixed")
gp_plot(gp, f, p, est$f, est$p, alt$f, alt$p, x_grid, obs, seed_i)
posteriors_plot(gp, priors) # needs trace=TRUE!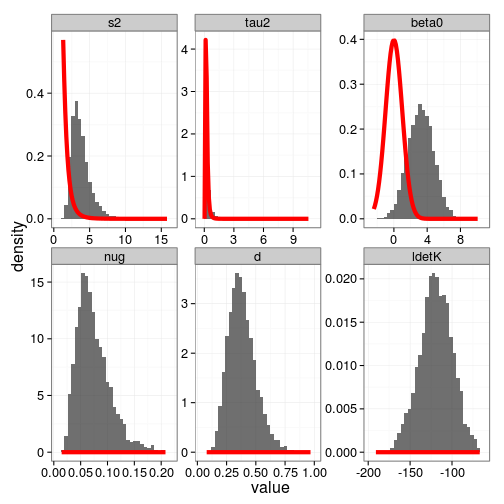
OPT <- optimal_policy(gp, f, est$f, alt$f,
p, est$p, alt$p,
x_grid, h_grid, sigma_g,
sigma_g, sigma_g, # est$sigma_g, alt$sigma_g, but those ests are poor
delta, xT, profit, reward, OptTime)
plot_policies(x_grid, OPT$gp_D, OPT$est_D, OPT$true_D, OPT$alt_D)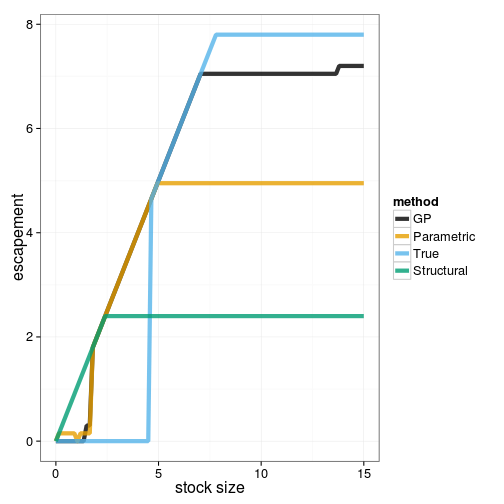
dt <- simulate_opt(OPT, f, p, x_grid, h_grid, x0, z_g, profit)
sim_plots(dt, seed=seed_i)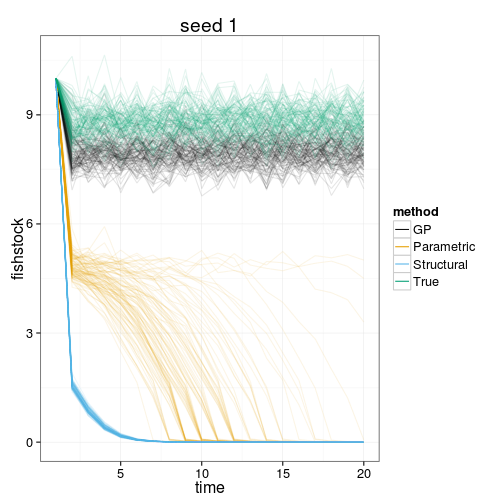
profits_stats(dt) method V1 sd
1: GP 19.337 1.6314
2: Parametric 6.446 0.3384
3: True 20.701 1.8012
4: Structural 7.650 0.0000