pdg-control
Problem statement: Maximize profits subject to \[\max_{h(t)} \int_0^T e^{-\rho t} \pi(x, h, t) dt \] Subject to the state equations (biology):
\[ \dot x = x \exp \left( \alpha \left(1-\frac{x}{K}\right) \left( \frac{x-C}{K} \right) \right) - x h \]
Note that we consider the control variable to be effort, \(h\) instead of harvest, \(\mathcal{H}\), where \(\mathcal{H} = h x\).
and the constraints: \[ x(0) = X_0 \qquad x(T) = X_T \] We have fixed boundary conditions (equalities) and equalities in the state equations, so we have a nice straight-forward problem. We assume the instantaneous profit function shows diminishing returns (i.e. satisfies the curvature conditions \(\frac{d \pi}{dh} < 0, \frac{d^2 \pi}{dh} > 0\)). For instance we could take the saturating function: \[ \pi(h, x, t) = \frac{h^{1+\gamma}}{1+\gamma} \] with \(\gamma < 0\). From this we can write down the associated present-value Hamiltonian: \[ H = \pi(h) - \lambda f(x,h) \] and the costate equation: \[ \dot \lambda = -\partial_x H = \lambda \left( \rho - \partial_x f(x,h) \right) \] and boundary conditions. Given our curvature assumptions on $ $, the maximum principle of Pontryagin gives us the first-order condition: \[ 0 = \partial_h H = \partial_h \pi - \lambda\] Assuming functional form above for fishing profits \(\pi\), we can then rewrite the costate equation. \[ \frac{d\lambda}{dt} = \frac{d\lambda}{d h}\frac{d h}{dt} = \gamma h^{\gamma} \frac{dh}{dt} = h^{\gamma} \left( \rho - \partial_x f(x,h) \right) \] simplifies to an ODE for $h $, leaving us with the two dimensional ODE BVP: \(\dot h = \gamma^{-1} \left( \rho - \partial_x f(x,h) \right)\) \(\dot x = f(x,h)\) \(x(0) = X_0 \qquad x(T) = X_T\)
Which we can solve by a variety of direct or indirect approaches. Note that we have analytically for \(f(x)\) given above \[ \partial_x f = - \alpha \frac{ ( C K - 2 x K - 2 x C + 3 x^2) }{ K ^ 2 } - h \]
For instance, solving with shooting or basic collocation:
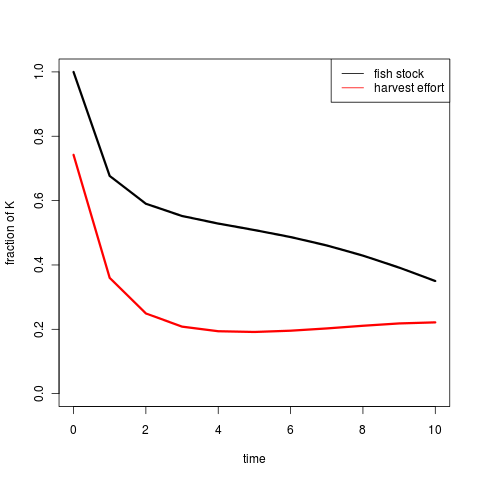
(code)