In this tutorial we walk through how to use the likelihood-based approach of Boettiger & Hastings (2012) to provide an early warning signal for a critical transition, and how to generate ROC curves discussed in the same paper for comparing different early warning signals. Context and details about the methodology are presented in the paper; here we focus on using the methodology provided in the accompanying R package. All of the examples shown here can be reproduced by pasting the code provided into an R terminal. We will need the following libraries to run this example. If you don’t have them, they can be installed from CRAN using the install.packages function.
library(ggplot2)
library(reshape2)
library(multicore)
library(devtools)We will be using custom functions provided in the R package Boettiger, (2012) that accompanies Boettiger & Hastings, (2012), which can be installed directly from the development repository on GitHub:
install_github("earlywarning", "cboettig")
library(earlywarning)We begin by loading the ibm_critical data provided in the package (from an individual-based model simulation of a critical transition). We plot the raw data to take a look at it.
data("ibms")
plot(ibm_critical, type="b")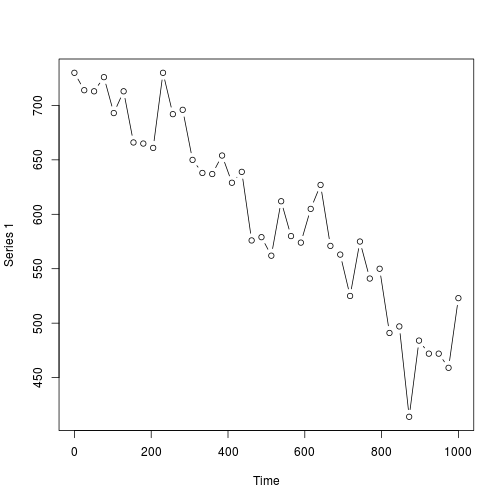
Fit both models to the original data, record the observed likelihood ratio of the original data
A <- stability_model(ibm_critical, "OU")
B <- stability_model(ibm_critical, "LSN")
observed <- -2 * (logLik(A) - logLik(B))Perform the bootstrapped model comparison on the parallel cluster.
runtime <- system.time(
reps <- mclapply(1:200, function(i) compare(A, B)))Which took 4176.78 seconds to run for the example shown here.
A helper function extracts the likelihood ratios under each of the pairwise comparisons (The null distribution: -2 times the log likelihood of data fit under A that had been simulated under A, minus the log likelihood of fits under A simulated under B; and the test distribution: fit under B when simulated under A, minus the loglikehood of being fit under B, simulated under B) as a data frame. we show the top of the data frame as output below.
lr <- lik_ratios(reps)
head(lr)## simulation rep value
## 1 null 1 0.001659
## 2 test 1 2.255139
## 3 null 2 1.892615
## 4 test 2 9.804084
## 5 null 3 4.795269
## 6 test 3 22.696982We use this data to generate the overlapping distributions shown in Boettiger & Hastings, (2012),
ggplot(lr) + geom_density(aes(value, fill=simulation), alpha=0.6) + geom_vline(aes(xintercept=observed))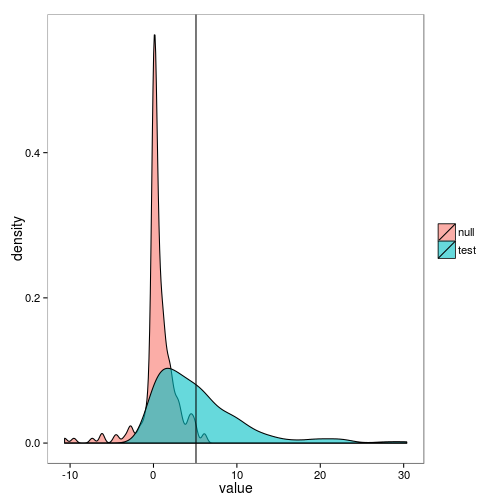
A second helper function generates the ROC curve from the likelihood ratio data, providing an alternative way to visualize this overlap:
roc <- roc_data(lr)
ggplot(roc) + geom_line(aes(False.positives, True.positives))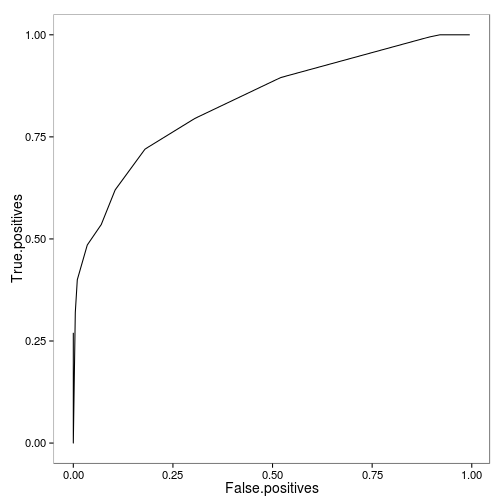
ROC curves are particularly useful in comparing the power of a variety of approaches. For instance, we can compare the performance of the likelihood-based signal shown above to the traditional approach of using a correlation coefficient to detect the increase in some summary statistic such as variance or autocorrelation. To obtain replicates, we will still simulate under the null (OU) and test (LSN) models estimated above, but instead of computing the likelihood of these data, we will estimate the commonly used rank correlation coefficient, Kendall’s tau, to quantify the increase in variance, autcorrelation, and skew observed in a moving window over the data.
var <- bootstrap_trend(ibm_critical, window_var, method="kendall", rep=200)
acor <- bootstrap_trend(ibm_critical, window_autocorr, method="kendall", rep=200)
skew <- bootstrap_trend(ibm_critical, window_skew, method="kendall", rep=200)These data are formatted like the likeihood ratio data above, only that the statistic is now Kendall’s tau.
ggplot(var) + geom_density(aes(value, fill=simulation), alpha=0.6) + geom_vline(aes(xintercept=observed))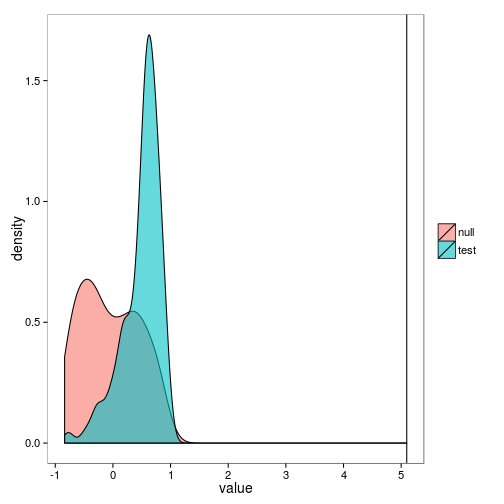
We can combine the data for the ROC curves of each indicator to compare:
indicators <- melt(list(var = roc_data(var), acor = roc_data(acor), skew = roc_data(skew), lr = roc), id = c("Threshold", "False.positives", "True.positives"))
ggplot(indicators) + geom_line(aes(False.positives, True.positives, color=L1)) 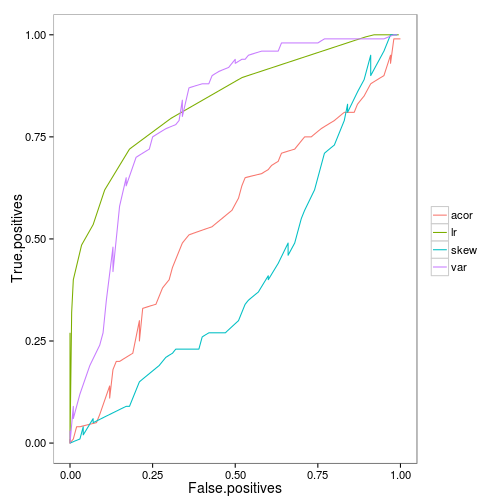
- C. Boettiger, A. Hastings, (2012) Quantifying Limits to Detection of Early Warning For Critical Transitions. Journal of The Royal Society Interface 9 2527-2539 10.1098/rsif.2012.0125