Critical transitions
Must determine the correct set of comparisons:
- Solve the SDP optim using the exact time dependent
- Simulate under an f with the same escapement policy but different functional form, i.e. logistic with K & r estimated from the May example, either analytically or directly from the data.
- Considering the costs of “cautious policy” (calculates optimal harvest recursively but always selects a fraction P of the optimal.) Results in non-constant escapement rules:
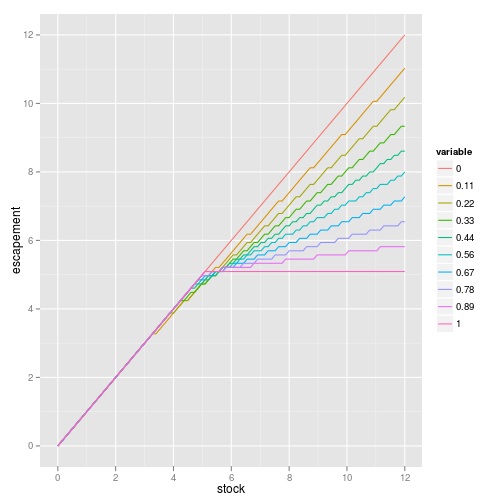
Also has nonlinear (convex) impact on value.
Filing out the boxes:
- the value of no action, no shift – NPV under assumed model
- the value of no action, shift – depends when shift occurs. Assume worst?
- value of action, no shift – Action is p = ?
- value of action, shift – action is p = ? Under what shift process?
- Consider the single-timestep decision first. Then the repeated decision.
Value of information
- logistic, lognormal (any measurement error is most conservative, then determinstic. gi the least)
- Beverton-Holt, lognormal (early version of figures) deterministic is least conservative, measurement errors, combined errors most. (Rerunning as bh_lognormal.Rmd)
- logistic, uniform (deterministic is always most conservative. gi is least)
Beverton-Holt, uniform (deterministic is most conservative, growth noise is least!)
constructed bias table: optimal under low/med/high r by implement under low/med/high r. (results)
rfishbase revisions
- add fair use text, future development with fishbase.org. DONE
- add all dependencies. DONE
- Reply letter text, send to P and D. DONE
- switch to robust regression. DONE
- fix/tweak figure appearance. DONE
- Resubmit.
Treebase
- Finish updates based on Duncan’s suggestions. DONE
- Submit 0.0-6 to CRAN. DONE
- Submit manuscript. DONE
Working on / To Do
- rfishbase – revisions. DONE
- evolution talk
- ievobio talk
- csgf talk
- esa talk
- wrightscape
- Alan decision theory and early warning
- Jim’s precautionary paper JEEM
- PDG policy costs
- Jake uncertainty and learning