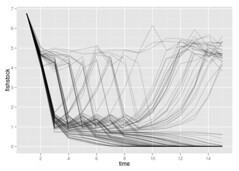
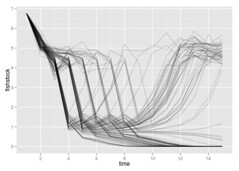
Have finally gotten my active adaptive management solutions working.
The active adaptive management solution learns very quickly and rather monotonically which model is correct, even when models differ by small amounts and the initial belief is heavily skewed to the wrong model. I’ve implemented examples with Myers model, but in this parameter space the allee effect is well below the Reed escapement level of the alternative Beverton Holt model, so it doesn’t exert itself.
- A case of choosing between to Beverton Holt models with very similar parameters. Some delay occurs before a given replicate observes an event unlikely to have come from the wrong model, and then it quickly adjusts its beliefs.
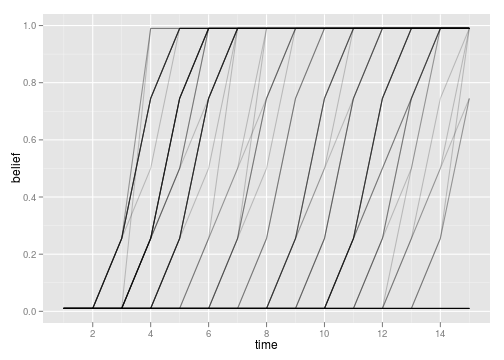
- Choosing between Beverton Holt and Myers Allee model. Allee model is correct even though our initial belief doubts it. The algorithm quickly corrects this.
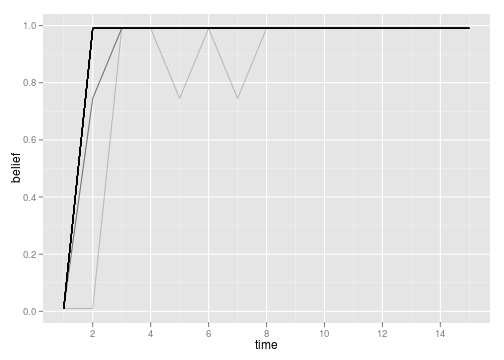
- Perhaps the most dramatic example I have so far comes from a mistake in my model specification, whereby what I intended to be the correct model was actually a terribly optimistic model. The algorithm quickly realized that it would do best to chose what I had provided as the wrong model, which was actually closer to the truth than my faulty specified true model.
\[ S = \frac{\alpha S ^ {\delta}}{1 + S^{\delta}/K} \] \[ 1 + S^\delta/K = \alpha S ^ {\delta-1} \] \[ K - K \alpha S ^ {\delta-1} + S{^\delta} \] for $ = 2 $ \[S = \frac{1}{2} \left( \alpha K \pm \sqrt{\alpha^2 K^2 - 4 K}\right) \]
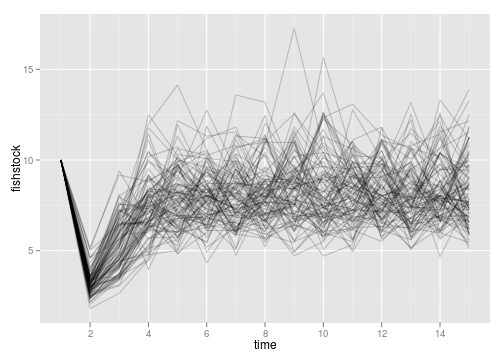
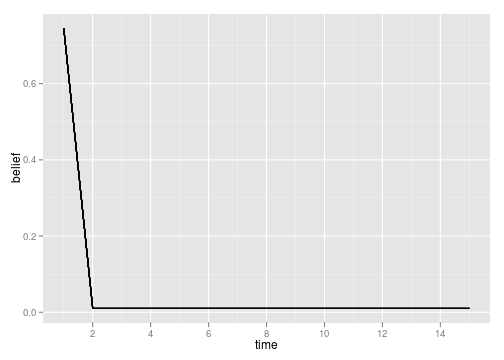
Cases where risk of collapse is real, learning is fast, but model uncertainty isn’t the challenge. Compare outcomes starting with wrong and right initial belief. Learning takes place in the first step, but many populations crash by chance anyhow.