So I’ve simulated 1000 replicates of a system that has alternative stable states, but is not approaching the bifurcation. I’ve added enough noise (demographic stochasticity in this case, but doesn’t matter what) that 129/1000 transition stochastically to the bad state, so I have decent sample sizes in each. 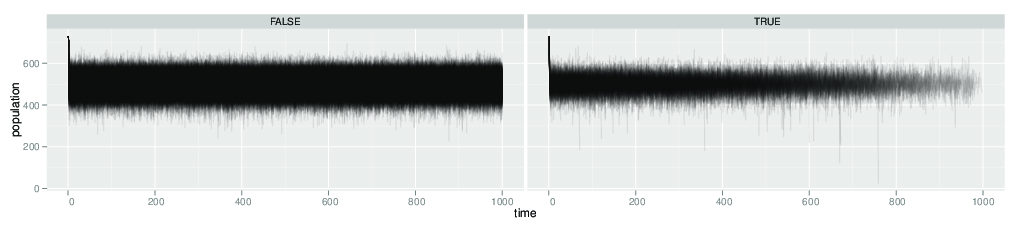
Here’s what I’m finding: If I condition on having crashed (i.e. take the 129 that transition) and apply our model-based early warning signal, it doesn’t detect any early warning sign. Meanwhile, if I apply the kendall’s tau to the trend in variance on both crashed and and un-crashed data, the distributions look more or less as they always do, with tau values covering the full range from -1 to 1. The statistic from the systems that did not crash (0) and those that did (1), for both the model approach (parameter m) and tau for variance trend).

Visually, I can also create the plot of the warning signal over time for those 129 sets, and some appear to increase.

So in this sense we can illustrate a prosecutor’s fallacy in the sense that some of these 129 appear as false positives; there variances increase by chance. However, this doesn’t show any effect of conditioning on the fact that the system has transitioned – by these statistics the group that did crash and the group that didn’t look indistinguishable. In this sense it’s no so much a fallacy.
I can try finer time sampling and see if I can catch a pattern that distinguishes between the groups – in the data I’ve got so far the chance fluctuation that drives the crash occurs faster than the observation rate, so there’s not much to latch on to.