The optimal policy with symmetric L1 costs to changing the quotas results in the solutions that stop changing, sometimes at no harvest (if there’s scrap value), or at some fixed high harvest if no scrap value. (See earlier notes). Asymmetric costs of comparable magnitude result in more crashes.
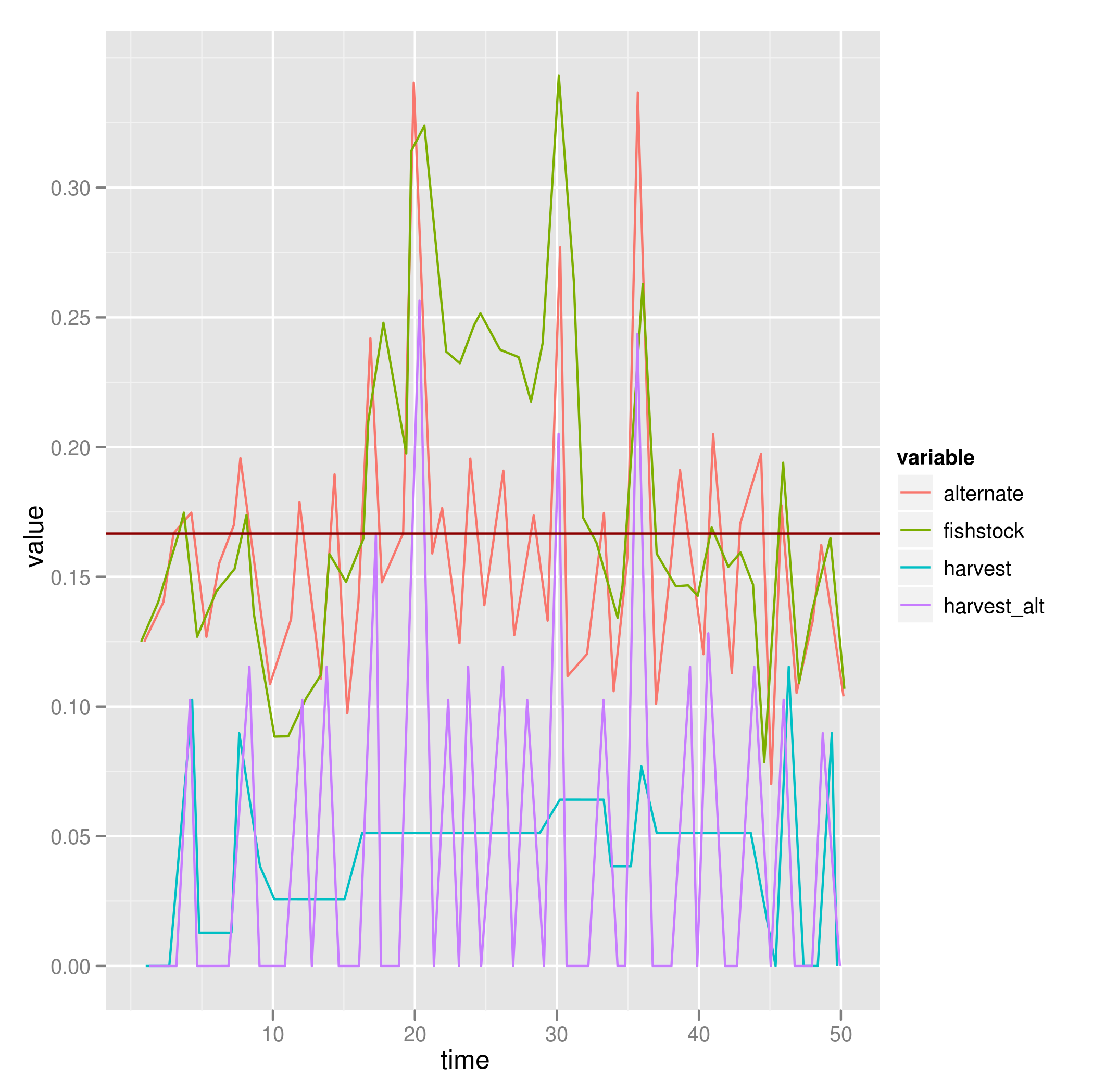
When we apply an L1 norm cost of the same magnitude as before for decreasing quotas, but allow increasing quotas to be free (no cost to environmental lobby), the solution follows the Reed optimum is in purple (harvest_alt) (cost-free adjustment), while the blue is the harvest level being implemented with a cost:

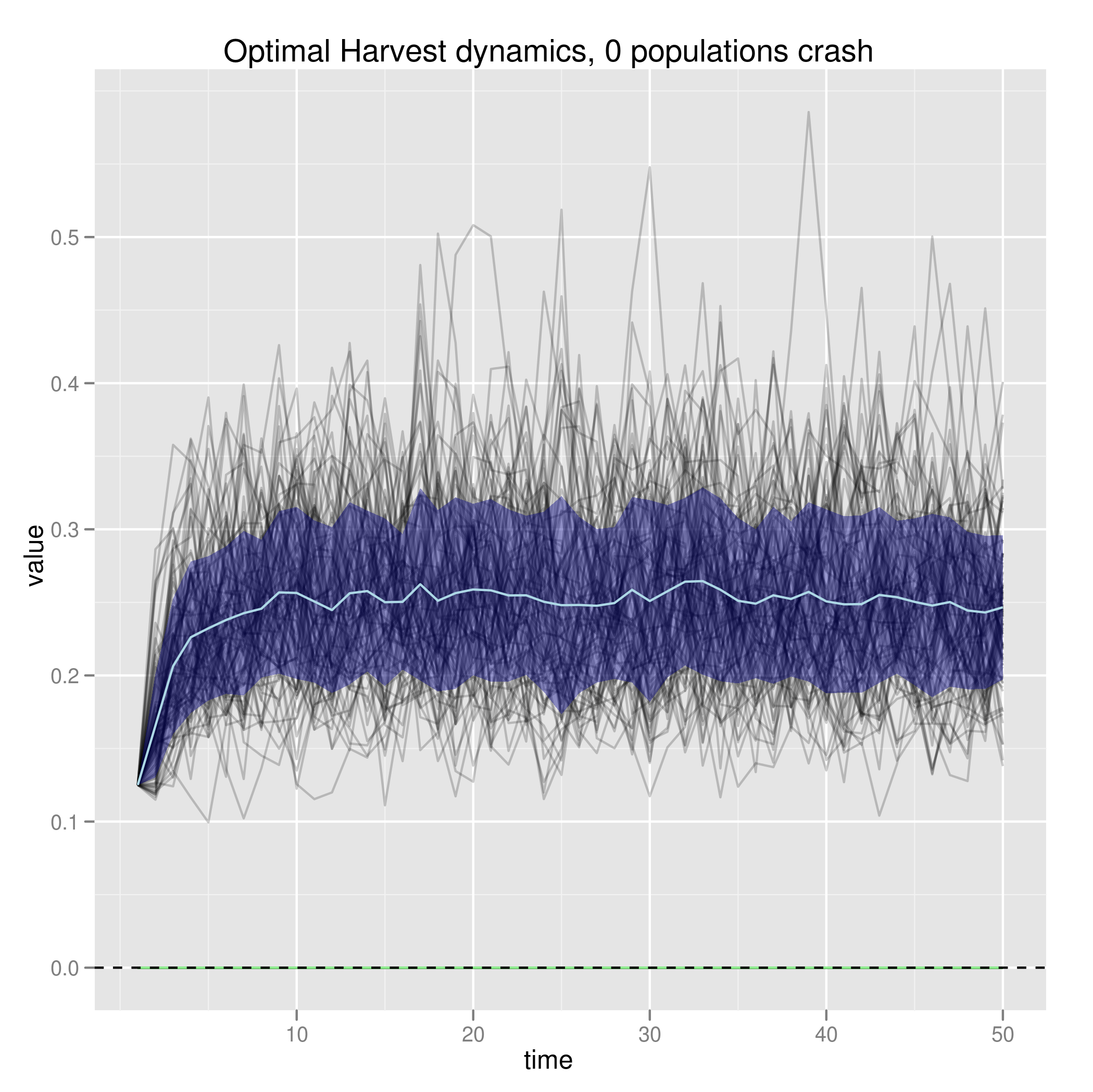
This is for a single replicate, but we can verify this holds across an ensemble of 100 runs:
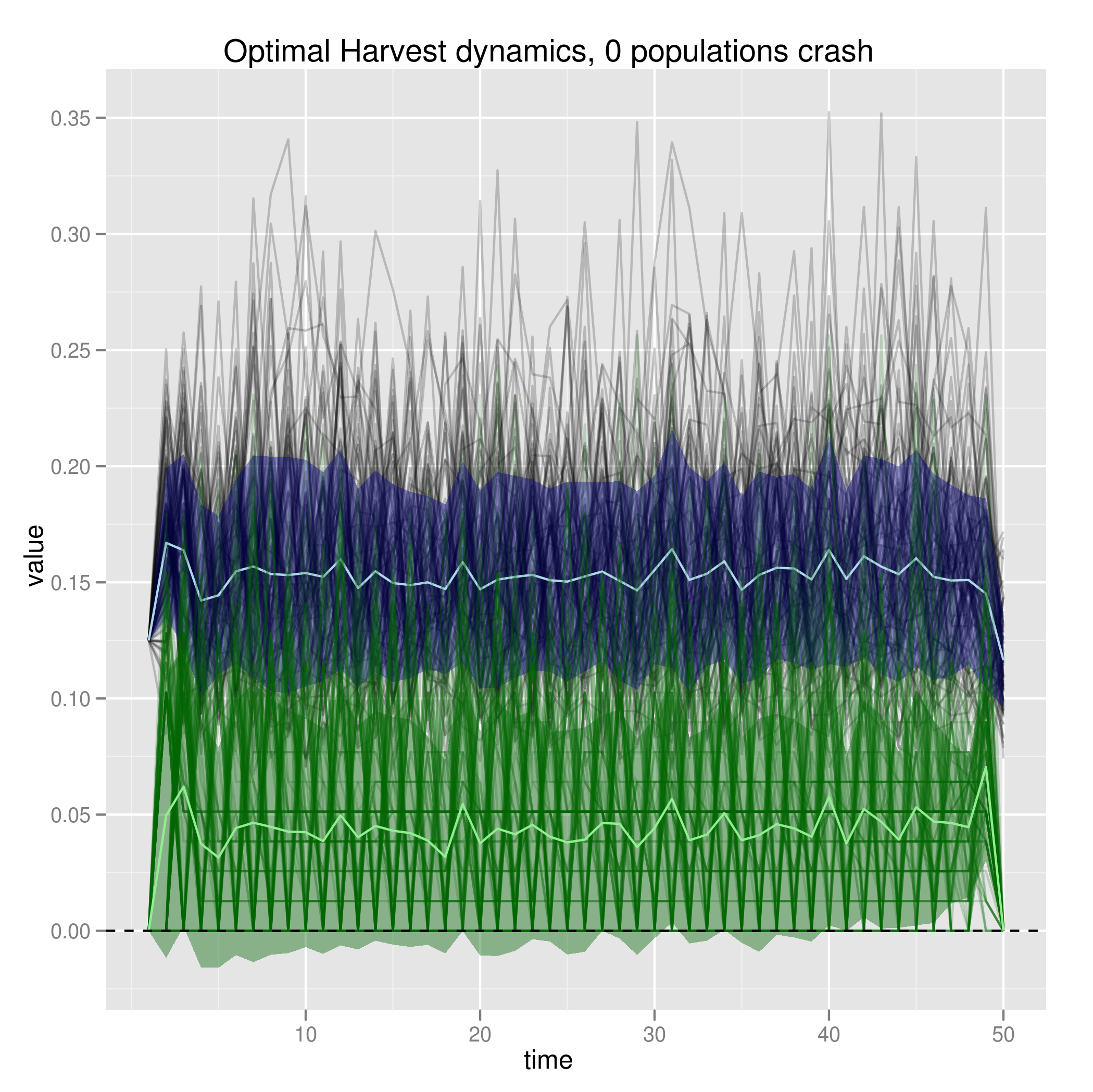
This is the same as the symmetric case when cost is relatively small. Since this case has the same cost to decrease quotas but no cost to increase quotas, it is overall a less expensive world in which to do business.
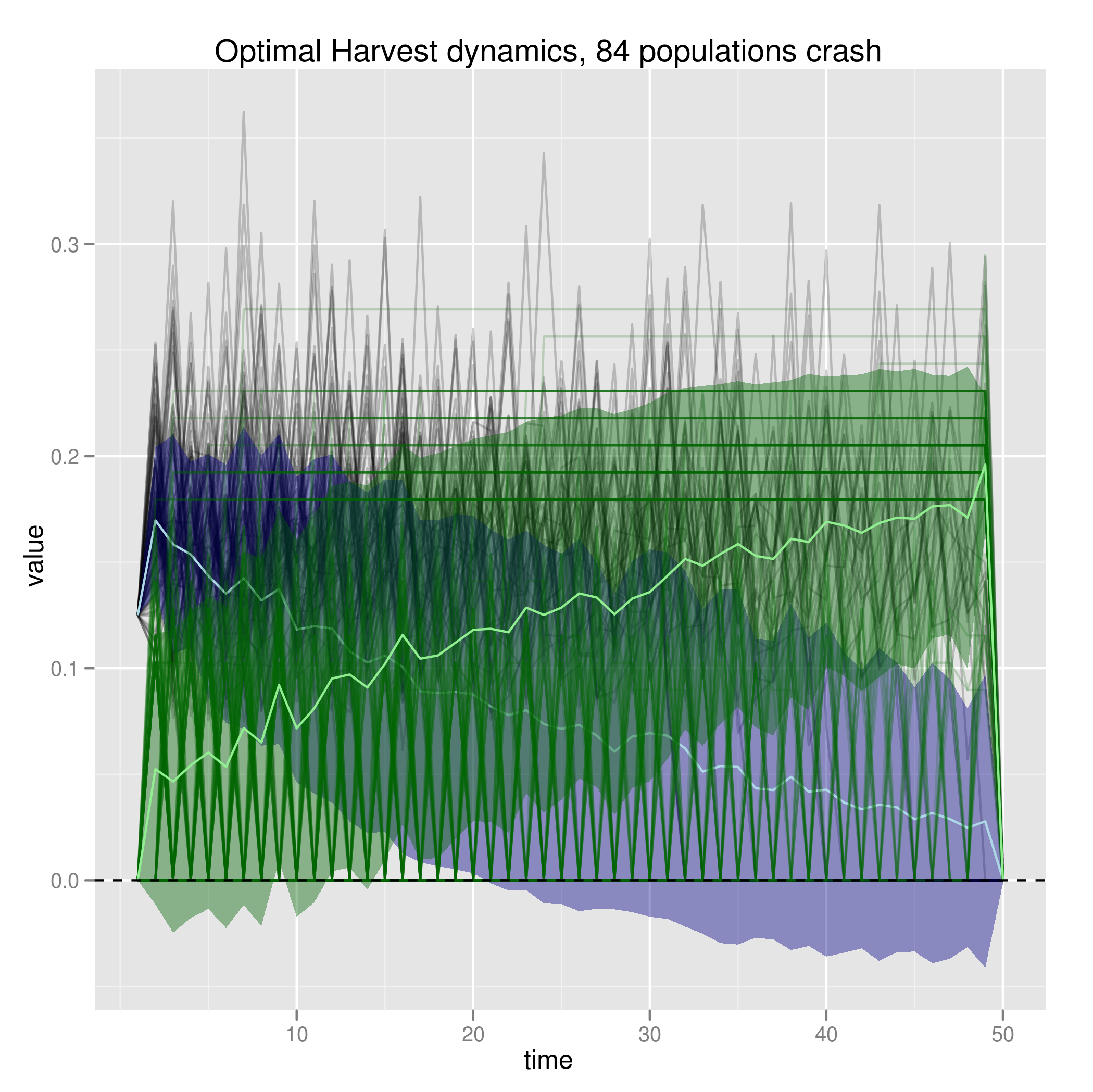
Asymmetric Policy costs lead to more population crashes
Just tried this and we do indeed see policies that deviate from the Reed optimum (harvest_alt), with the blue harvest line changing far less often, but decreasing by amounts that seem about the same as the increases.
The ensemble shows the tossing in the towel result of the symmetric case, where several of the replicates cease any changes at all and just send the population to 0 after a certain point.
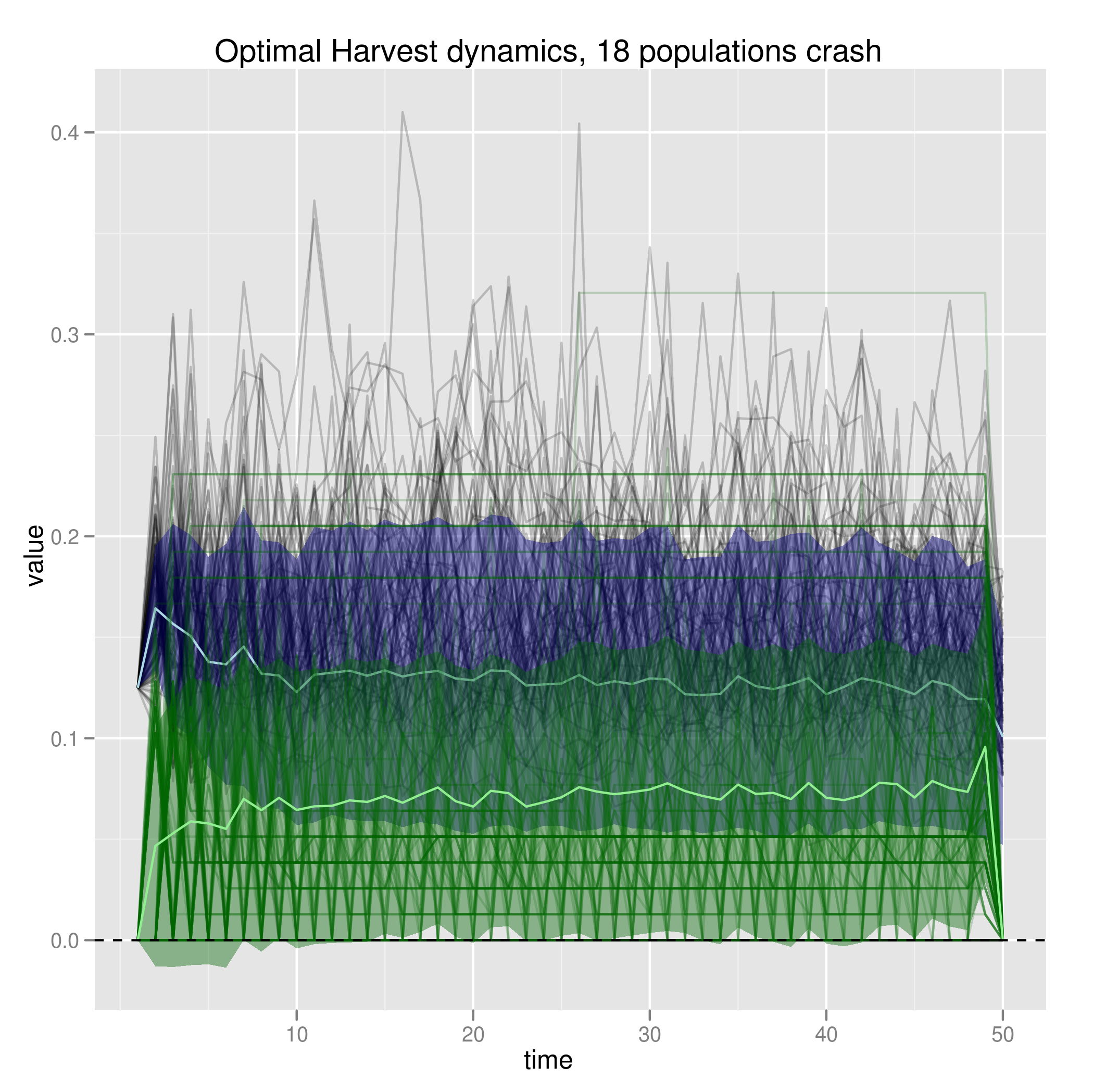
This is indeed worse than the optimum solution with symmetric costs at a matching penalty, where the solution is not to harvest
In these cases there is a fixed reward / scrap value for not crashing the population.
No scrap value
Symmetric costs with no scrap value result in this “tossing in the towel” pattern of following the Reed policy for a while, and then leaving a constant harvest high rate that crashes the stock.
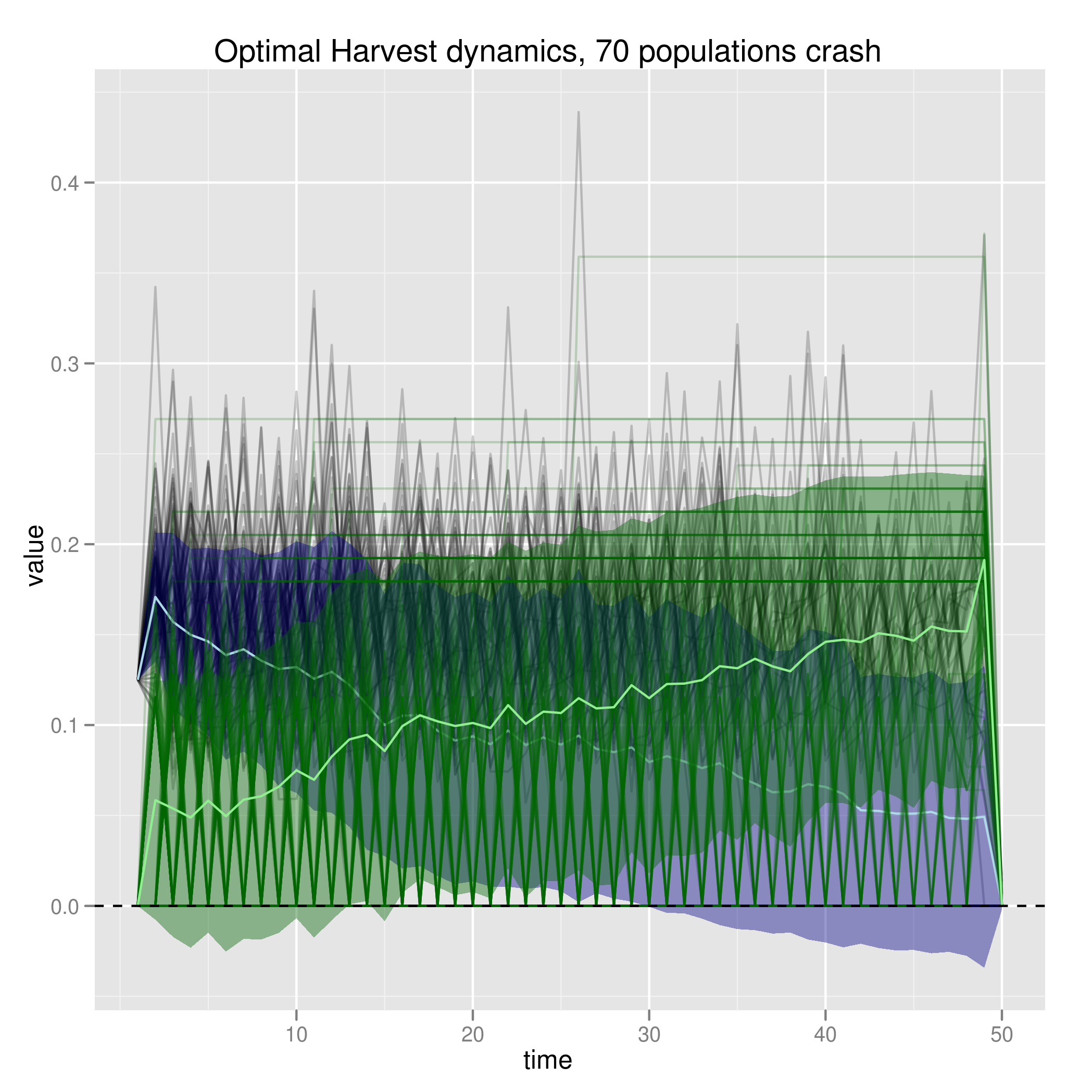
Running the asymmetric costs with no scrap value, we find everything crashes immediately:
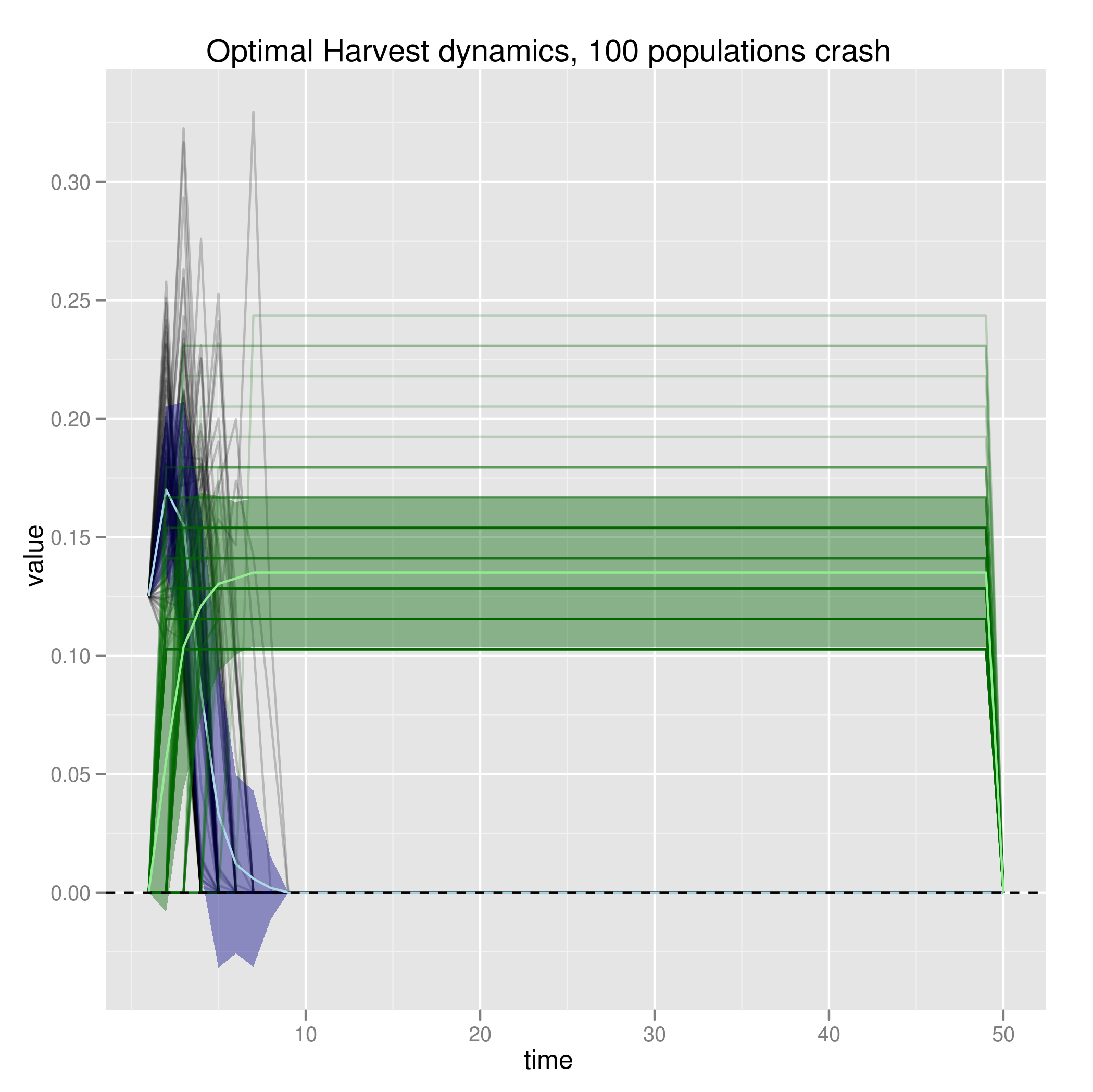
Replicating this with costs 1/10th as high does this more gradually.