Peter posed an interesting question to me this afternoon: can we infer a model in which the rate of evolution in one trait (say, its Brownian diversification rate parameter) depends on the value of another trait (say, linearly and assume the other trait depends on Brownian motion). Without all those assumptions we write this generally as:
\[ dX_t = f_x(X_t, Y_t) dt + \sigma_x(X_t, Y_t) d W_t \] \[ dY_t = f_y(Y_t) dt + \sigma_y(Y_t) d W_t \] (subscripts do not imply derivatives in my notation)
Adding the assumptions: \[ dX_t = \sigma_x \sigma_y Y_t d W_t \] \[ dY_t = \sigma_y d W_t \]
I believe this is non-linear, hence the distribution of trait values is not Gaussian. Perhaps this should be obvious, but late on a Friday let’s simulate (see code), and just look at the QQ-plot: 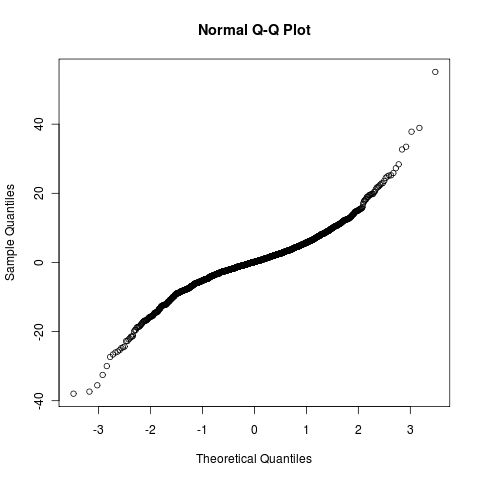
This means the distribution of trait values on the tree under the model will not be multivariate normal, unlike the case for all other nicer models we’ve considered. I thought a transformation might save this, but I’m unfamiliar with multidimensional Lamperti transform and haven’t come across any good coverage of it, either on the web or in Oksendal or Iacus. Anyone?
–Added note: Yes, this is obvious. as this is the product of two Gaussian processes, it is not Gaussian. Still, looks simple enough to have a closed form solution…
A related one-dimensional model
In one dimension we can have a trait value which influences its own rate of diversification:
\[ dX_t = f(X_t) dt + \sigma(X_t) dW \]
And by applying a rarely discussed method known as the Lamperti transform, turn this into a linear function in a new variable:
\[ Y = \int_z^X \frac{1}{\sigma(u)} du \]
Then by Ito formula we find the Lamperti transform: \[ dY = \left( \frac{f(X_t)}{\sigma(X_t)} - \frac{1}{2} \partial_x \sigma(X_t) \right) dt + dW_t \]