Looks like my troubles actually stem from a bug in the code. I summarize the problem here, just as I posted in my query to R sig phylo. Essentially the program erroneously squares alpha at the moment, explaining the pattern I found yesterday. Giving it root alpha preemptively should be a good work around.
~~ {.de1} data(bimac) tree <- with(bimac,ouchtree(node,ancestor,time/max(time),species)) print(h2 <- hansen(log(bimac[‘size’]),tree,bimac[‘OU.1’],alpha=1,sigma=1)) ~~
The print command says alpha = 0.1921554 The call h2@alpha says alpha = .4383554
which is the sqrt of the other. Certainly these should all agree. The summary command agrees with the print command:
smry = summary(h2)
smry$alphaA little exploration seems to show that the print command is the correct one. If we want to simulate a model with a particular alpha value, we first have to generate a fitted model as above, then update the alpha value and call simulate on the fitted model. I believe ouch is accidentally squaring the value of alpha we give it before running the simulation. For example:
> h2@alpha = 5
> replicates <- as.data.frame(simulate(h2, 1000))
</syntax>
I find the expected variance by averaging the variance across the replicates,
<syntaxhighlight>
> mean(sapply(1:1000, function(i){var(replicates[i], na.rm=T)} ) )
[1] 0.0009774488So did it use 5 or 25 as the alpha value? Since either value is large compared to the length of the tree, the tip variance should be stationary independent of tree structure so we can check it against the analytic predicted variance (sigma^2/2 alpha):
> (h2@sigma)^2/(2*h2@alpha)
[1] 0.004836469
> (h2@sigma)^2/(2*(h2@alpha)^2)
[1] 0.0009672938As the second equation agrees with the simulation, it believe that ouch has erroneously squared the value of alpha in the simulation.
Limits to Power in Trees
Now that I’m sure I can compare apples to apples (matching stationary distributions), I can finally perform my intended comparison.
- First, confirm that the distributions generated by the models on the star tree are indistinguishable:

- Next, the same models are distinguishable on the Felsenstein Tree:
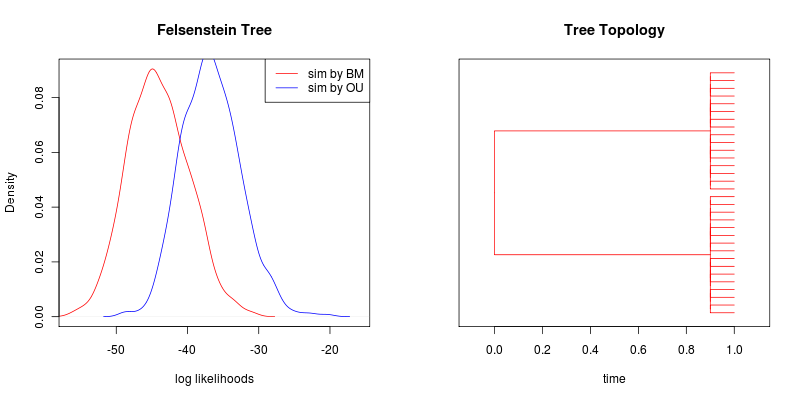
Here α = 1 and σ = 3
Intuition at the moment: The longer the two branches before the polytome in the Felsenstein tree, the more powerful the tree will be. More precisely, we can ask what is the smallest value of alpha that can be reliably distinguished from BM on this particular tree? That answer should be proportional to how close the variances of two branches can get to their stationary values, 1 − e^−\ 2αs^ where s is the branch length, 0.9 in this case, giving us 83% of the way to the equilibrium.
Compare moving the branch points from t=0.9 to t=0.45 vs halving alpha:
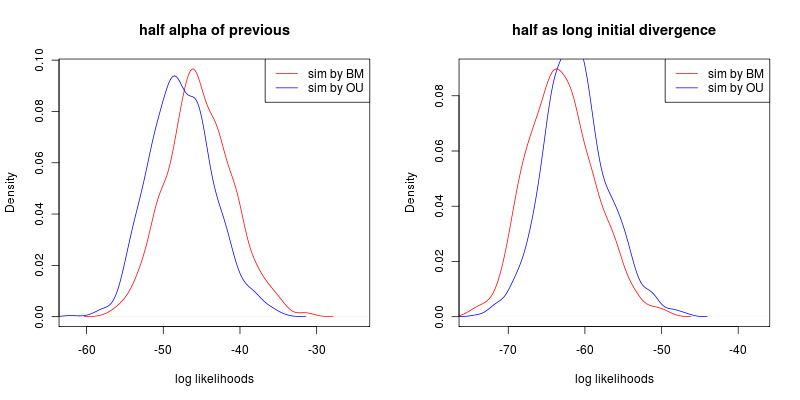
Both show an roughly equal reduction on the discriminatory power, and the ability to discriminate between models is lost.
- On the flip size, we can increase the power by doubling alpha from 1 to 2,

- Still need to explore the effect of simply increasing the length of time in the entire tree, doesn’t match doubling alpha. Increasing alpha also tightens the distribution, so reaching the stationary distribution along the branch isn’t enough.
Computational Comments ———————-
Have started using google style guidelines for R code. Will also be implementing google style for C.
SVN log
r214 | cboettig | 2010-03-03 18:43:28 -0800 (Wed, 03 Mar 2010) | 2 lines
final version of the day. continues tomorrow…
r213 | cboettig | 2010-03-03 17:48:33 -0800 (Wed, 03 Mar 2010) | 2 lines
figure three: weaker
r212 | cboettig | 2010-03-03 17:29:29 -0800 (Wed, 03 Mar 2010) | 2 lines
code for felsenstein_tree.R as produced the first two plots in today’s entry, about to modify for plots 3 and 4
r211 | cboettig | 2010-03-03 15:52:37 -0800 (Wed, 03 Mar 2010) | 2 lines
resolved problem discussed in yesterday’s entry, see todays entry
r210 | cboettig | 2010-03-03 01:23:14 -0800 (Wed, 03 Mar 2010) | 2 lines
Commiting version that appears in March 2nd notes