Meeting with Graham and Peter

Primary focus of today’s discussion was rooted in Sunday’s entry

On plotting quirks, haven’t figured out lattice but here’s yet another newer plotting engine for R
I need to revisit how OUCH computes likelihood ratios and P values. Since some parameters are bounded to the positive real line (and may be small) the standard chi square isn’t correct. I should repeat the AIC-style analysis for likelihood ratios, though this is just a shift of where I put the zero line. The correct thing to do would be to ask what is the probability the observed difference in likelihood ratio (or AIC, etc) would have occurred by chance using the distributions I have calculated,

(click for larger)

The approach I am advocating for goes by the name Parametric Bootstrapping (that link isn’t that helpful actually, could improve the wiki entry). I should implement this as above, comparing to the observed differences in the model scores of the real data, rather than the measure of slightly greater which I report.
Using this approach I can also evaluate the power to detect any OU model by overlap in distributions. For instance, if the tree is the starburst, even strong selection OU will have no power, while on another tree it might. This can be done by testing a variety of OU models, rather than the one that best fits the data, and will be a great way to start quantifying the information contained in the tree relative to the model choice question. This is a crucial step before I try more complicated models, giving some measure of whether a tree contains enough taxa with enough covariance to tease out temporal information accurately.
Discussed my concern that the BM model and OU model aren’t really embedded, since the OU model likelihood cannot be computed accurately for small α. Of course it works in the limit, but is something to be cautious about. It has been suggested that model comparison should fit OU alone, and wait and see if α comes out small. There are two reasons to be skeptical of this

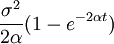
the star burst tree demonstrates that α and σ aren’t independent; then the tip variance is $\frac{\sigma^2}{2\alpha}(1-e^{-2\alpha t})$
The likelihood calculation may be numerically inaccurate for small α

So I can compute the joint probability for an arbitrary model rather quickly using my discretized matrix approach; if I’m given the transition matrices along each branch. Unfortunately, I spend all the computational time computing these matrices in the first place. We discussed several strategies to speed this up.

Look-up tables. For instance, rather than calculating 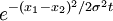$e^{-(x_1-x_2)^2/2\sigma^2t}$ I could use the look-up of 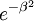$e^{-\beta^2}$ There’s a variety of places this kind of trick can help with. Also, judicious use of logs – never exponentiate when I can multiply, or multiply when I can add.
MCMC approaches. The general version of this just does MCMC over all the internal nodes. The key here is that if I know the values of all the internal nodes, the joint probability is just a product of all the transitions – no non-independence. Alternately, I could rely on the fact that I can solve this analytically if I were only told the regimes of the internal nodes, so I just have to MCMC over the handful of possible regimes at each node, and not the traits as well. This seems quite promising.
Going from the generator – this could be done for the truly nonlinear models, as it completely ignores the ability to get analytic solutions. The generator could be raised to the power of the branch length. Doing so for the largest branch would allow all other branches to be calculated in the process. This will probably be slow but easy to implement.

First: the the parametric bootstrap extension and paper.
- modification of the code I currently have to do likelihood ratio and compare to the true data.
- Also add a function to give scores to trees regarding ability to distinguish OU and BM models as a measure of the temporal information they contain.
Lookup tables – means that giant data structure I wrote for the regimes model will be useful, (yay and yikes). More memory and probably more time with valgrind debugging, but could be promising.
After that I think I’ll try MCMC over regimes and possibly the generator approach. An effective regimes calculation is probably a ways off yet, but plenty of things to try!